Appassionata di matematica e di “danza in volo”, la ballerina Erica Occhionero conseguirà la laurea magistrale in Matematica all’Università del Salento presentando la tesi “Un’introduzione al gruppo delle trecce anulari” e accompagnandola da una breve dimostrazione pratica: la discussione è in programma mercoledì 13 aprile 2022, alle ore16.15 nell’aula “Raimondo Anni” del Dipartimento di Matematica e Fisica “Ennio De Giorgi” (l’esibizione di danza in volo è prevista per le ore 16.30), nel complesso Ecotekne – ingresso dalla via per Arnesano.

          Erica Occhionero, leccese, 25 anni, è studentessa di Matematica a UniSalento e ballerina autodidatta di “danza in volo”. A causa di una frattura alla caviglia subita a 16 anni per un incidente stradale, è stata costretta a rinunciare alle scarpette ma, decisa a non smettere di danzare, ha cominciato a studiare la “danza in volo” utilizzando un’amaca di seta. Ha studiato parallelamente matematica, coniugando negli anni le due passioni. Vincitrice di vari premi e riconoscimenti, nel 2019 ha partecipato ai casting di “Ballando on the road” con Milly Carlucci ed è stata successivamente ospite di trasmissioni televisive sia sulla Rai nazionale che su emittenti regionali. «Nella matematica e nella “danza in volo” vedo profonda bellezza, eleganza e creatività», spiega, «Da qui l’idea di intrecciarle nella mia tesi: vorrei dimostrare che la matematica è ovunque, non è mai noiosa ma si evolve, e penso che la danza in volo sia una forma bellissima per descriverla. E quale modo migliore per comunicare, se non con una dimostrazione pratica?».

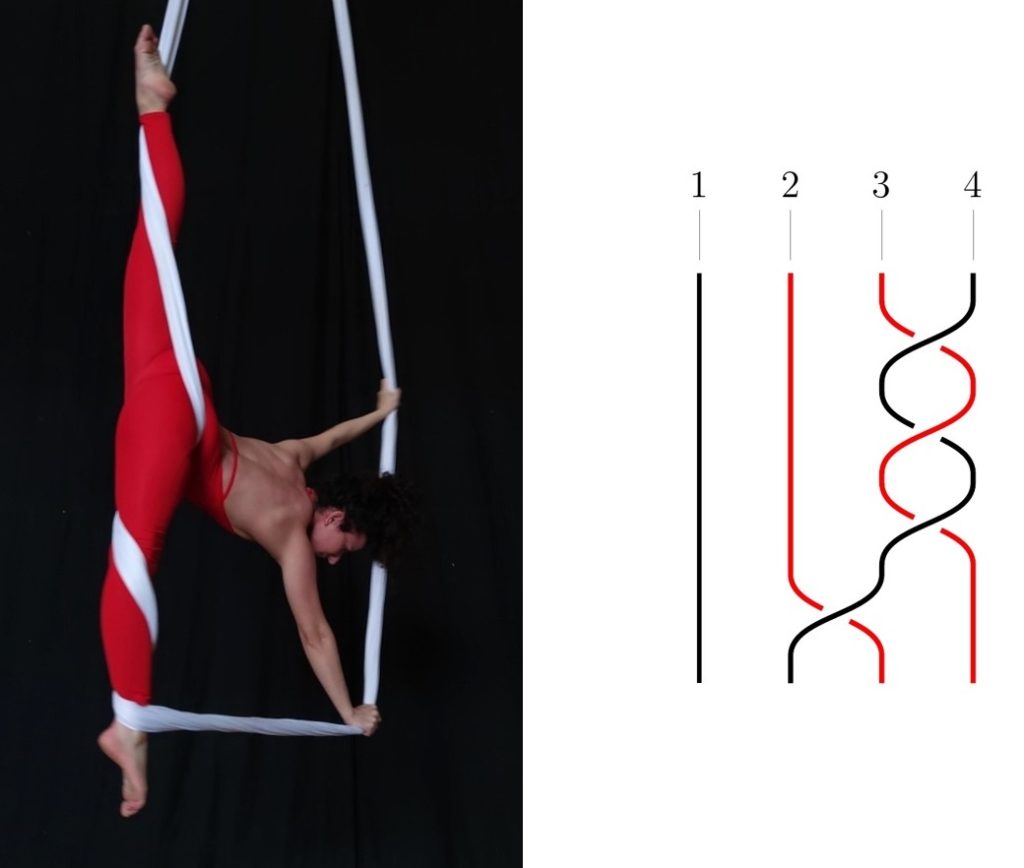
Il contenuto della tesi. Pensando alle trecce, vengono subito in mente le acconciature dei capelli o le decorazioni di articoli comuni come cinture, bracciali, forme di pane, cesti in vimini, tappeti e lavori a maglia. Oggetti così comuni hanno ispirato negli anni ’20 del Novecento una profonda teoria matematica, la “teoria delle trecce” appunto, molto ricca di risultati e di applicazioni e tuttora oggetto di studio. Le “trecce anulari” sono delle trecce le cui stringhe hanno la particolarità di potersi attorcigliare anche attorno a un sostegno fisso, detto in gergo “palo”. Ci si può fare un’idea concreta osservando la danza del “palo di maggio”, un rituale primaverile che affonda le sue radici nella storia europea. In questa cerimonia alcuni ballerini si muovono intorno a un albero al quale sono attaccati dei nastri di tessuto. Ciascun ballerino ha in mano l’altro lembo del nastro e, danzando secondo schemi ben definiti, intreccia i nastri creando una vera e propria treccia attorno all’albero. Far seguire una treccia anulare da un’altra treccia, cioè “comporre” due trecce, è un’operazione naturale in questo ambito. La “teoria delle trecce anulari”, che si è sviluppata molto dopo quella delle trecce classiche, assicura che ogni treccia anulare può essere ottenuta componendo un certo numero di trecce elementari. La teoria si fonda sullo studio di un oggetto matematico, detto il gruppo delle trecce anulari, che descrive e sintetizza tutte le possibili composizioni di trecce anulari elementari. L’individuazione di speciali insiemi, costituiti da numeri diversi di trecce elementari, che permettono di ottenere l’intero gruppo, è stato l’obiettivo principale della tesi di laurea magistrale in Matematica di Erica Occhionero, sotto la supervisione del professor Francesco Catino e della dottoressa Marzia Mazzotta. Ogni treccia anulare può essere rappresentata mediante un opportuno grafico piano, da cui si evincono le trecce elementari che compongono la treccia stessa. Tali grafici sono stati utilizzati dalla laureanda per tenere traccia dei movimenti da lei eseguiti nella creazione di diverse figure che costituiscono le varie coreografie della sua danza in volo.

          «La percezione generale che si ha della matematica è spesso quella di una disciplina astratta o, ancora peggio, arida», sottolinea il professor Giovanni Calvaruso, Presidente del corso di laurea in Matematica a UniSalento, «Invece chi fa lo sforzo di acquisirne il linguaggio e i metodi si rende conto della sua universalità. Grazie alla sua formazione riesce a vedere la trama matematica presente anche in ambiti apparentemente lontanissimi, come quello di un’attività artistica. La matematica è ovunque, e le sue applicazioni si fanno di giorno in giorno più vaste e profonde».

Lecce, 11 aprile 2022

di Redazione